題目介紹:
題目要求給定一個整數 n，生成一個Gray code sequence。
格雷碼是一種二進位編碼方式，使得任意相鄰兩個數字的二進位表示僅相差一個位元（bit）。
解題流程:
1.格雷碼的相鄰數字只差一個 bit
2.可用遞迴或迭代方式從前一層的格雷碼生成
3.結果長度為 2^n，第一個數為 0
程式碼及執行結果截圖: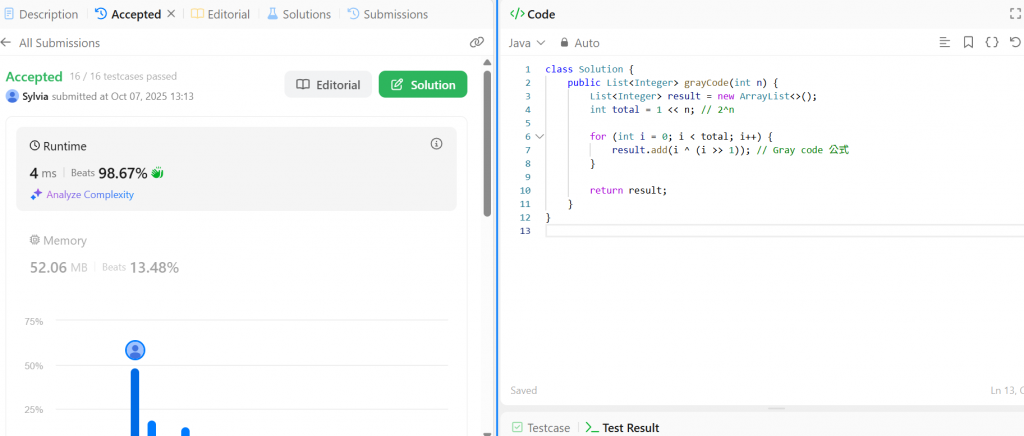

學習心得:
題目要求生成相鄰數字僅差一個 bit 的序列，剛開始我以為需要用遞迴或回溯方式來嘗試各種排列，但實作上容易出錯、效率也不高。後來了解到可以用公式 gray(i) = i ^ (i >> 1) 直接生成格雷碼，才發現原來問題背後隱藏著數學與邏輯的規律。這個題目讓我更熟悉了位移與 XOR 運算的概念，也理解了如何用簡潔的運算取代複雜的流程。
延伸邏輯時事面:
1.數位通訊與錯誤控制：
格雷碼在通訊與編碼領域被廣泛應用，因為相鄰代碼僅有一個位元變化，可減少訊號轉換時的錯誤，與現代 5G 通訊中「低錯誤率傳輸」理念相呼應。

2.機械與感測應用：
在工業自動化或機械感測器（如旋轉編碼器）中，格雷碼可避免因機械震動造成的多位誤讀，與現今智慧製造、機械精準控制技術的需求密切相關。

3.電腦科學中的效能與安全性：
格雷碼的位元變化特性有助於降低硬體功耗與干擾，也被研究應用於低功耗晶片設計及資料加密領域，呼應當前 AI 晶片與綠色運算的發展趨勢。